Цитата:
Сообщение от Jahongir Haitov

|
О! Помог наконец-таки рисунок Джахонгира, позволил сообразить (в отличие от моих :-))
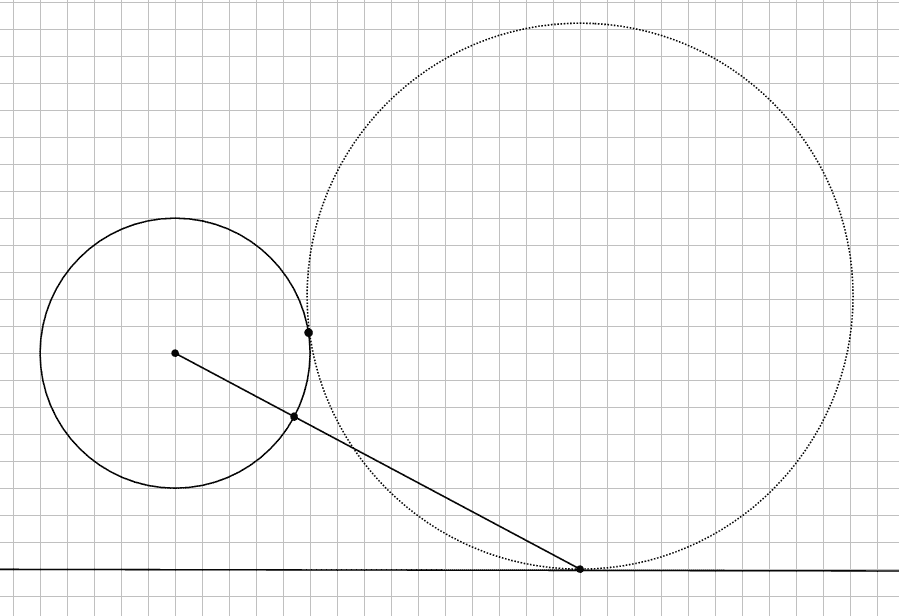
1. Проводим линию параллельно заданной и смещенной от окружности на растояние радиуса заданной окружности - пусть R
2. Из точки А восстанавливаем перпендикуляр к линиям - центр искомой окружности должен лежать на нем.
3. Соединяем точку пересечения перпендикуляра со сдвинутой линией (В) с центром исходной окружности (О), находим середину ВО и из нее восстанавливаем перпендикуляр до пересечения с перпендикуляром к исходной линии. То есть, мы нашли центр окружности, проходящей через точки О и В, а радиус этой окружности на R больше радиуса искомой окружности.
4. Зная центр проводим окружность из него - она пройдет через точку А и коснется нач. окружности. Вуаля! :-)














 Линейный вид
Линейный вид
