Старая задачка из Кванта

[Barbedo]

Рассмотрим нашу фигуру в двух проекциях:

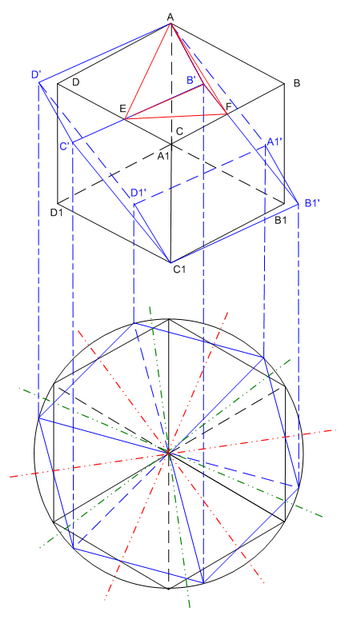
Обратим внимание на красные и зеленые штрих-пунктирные линии. Предствами себе, что мы обратно совместили оба куба, а затем начали поворачивать их вокруг главной диагонали в противоположные стороны синхронно. Тогда уходящие вправо части куба симметричны уходящим влево относительно неподвижного радиального луча. Вследствие этой симметрии при любом относительном угле поворота ребра кубов, не пересекающие главную диагональ, будут пересекать друг друга по линиям симметрии - красным и зеленым. Следовательно, можно считать доказанным, что общая часть двух кубов ограничена 12-ю равными треугольниками, общая площадь которых составит общую площадь поверхности фигуры, а общий объем двух кубов за вычетом объема 12-ти треугольных пирамид (см. AB'EF), отсекаемых кубами друг от друга, составит объем общей части кубов. Теперь можно перейти к вычислениям.