h=gt^2/2
Vo=gt
Vo=(2gh)^0,5
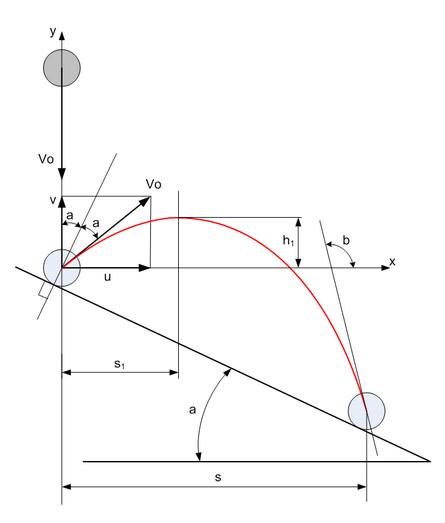
v=Vo*cos(2a)
u=Vo*sin(2a)
h1=vt1/2
s1=ut1
t1=v/g
h1=v^2/2g
s1=uv/g=Vo*sin(2a)*Vo*cos(2a)/g=Vo^2*sin(4a)/2g
Взяв за начало координат точку первого отскока, запишем траекторию шарика в виде:h(s)=-k(s-s1)^2+h1
При s=0 имеем:
k=h1/(s1)^2=(v^2/2g)/(uv/g)^2=g/(2u^2)
и уравнение параболы
h(s)=-g/(2u^2)*(s-s1)^2+h1
Уравнение наклонной плоскости запишем в виде:
y(s)=-s*tga
Точку падения шарика найдем при h(s)=y(s)
-g/(2u^2)*(s-s1)^2+h1=-s*tga
g/(2u^2)*(s-s1)^2-h1-s*tga=0
g/(2u^2)*(s^2-2ss1+s1^2)-h1-s*tga=0
g/(2u^2)*s^2-2sg/(2u^2)*uv/g+g/(2u^2)*(uv/g)^2-v^2/2g-s*tga=0
g/(2u^2)*s^2-sv/u+v^2/(2g)-v^2/2g-s*tga=0
g/(2u^2)*s^2-sv/u-s*tga=0
g/(2u^2)*s-v/u-tga=0
s=(v/u+tga)/(g/(2u^2))=
=2(ctg(2a)+tga)*u^2/g=
=2((ctga-tga)/2+tga)*u^2/g=
=(ctga+tga)*u^2/g
Тогда t полета шарика между первым и вторым ударом о плоскость составит:
t=s/u=(ctga+tga)*u/g=(ctga+tga)*Vo*sin(2a)/g=
=2Vo(ctga+tga)*sina*cosa/g=
=2Vo(cos^2(a)+sin^2(a))/g=2Vo/g
Т.е. получилось, что время полета шарика между первым и вторым ударом о наклонную плоскость не отличается от аналогичного времени при ударе о горизонтальную плоскость независимо от угла наклона плоскости к горизонту! Но это для вертикального падения шарика.
Теперь второй отскок шарика.
Определим угол второго падения шарика как угол между касательной к первой параболе и горизонтом в точке падения.
S1=ut=u*2Vo/g
tgb=h’(S1)=(-g/(2u^2)*(S1-s1)^2+h1)’=
=-g/(u^2)*(S1-s1)=
=-g/(u^2)*(u*2Vo/g-uv/g)=
=-(2Vo-v)/u=
=-(2Vo-Vo*cos(2a))/(Vo*sin(2a))=
=-(2-cos(2a))/sin(2a)
Дальше при подсчете времени никак не удается избавиться от а. Похоже, что время между отскоками, начиная со второго, будет меняться.
Может, нахомутал где...








 .
.
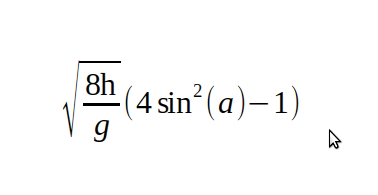





 Линейный вид
Линейный вид
