Цитата:
Сообщение от Barbedo

было бы крайне интересно решить задачу на плоскости, без выхода на конус и его проекции.
|
Как я сказал выше, точка , которая, во-первых, лежит на прямой PQ, и ,
во-вторых, находится на одинаковом расстоянии от фокуса F и директрисы d является искомой точкой пересечения параболы и прямой, так как она удовлетворяет основному свойству параболы и тем самым, принадлежит ей.
Мы рассмотрим случай, когда PQ пересекается с директрисой.
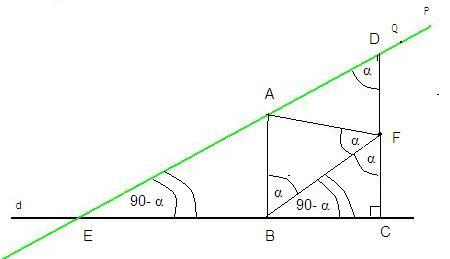
Построение.
Продолжим прямую PQ, до пересечения Е с директрисой.
Построим прямую, проходящую через фокус Е перпендикулярно d. Пусть она пересекается с директрисой d в точке С, а с прямой PQ в точке D.
Построим прямую, проходящую через фокус Е параллельно PQ. Пусть она пересекается с директрисой d в точке В.
Построим прямую, проходящую через В перпендикулярно d.. Пусть она пересекается с прямой PQ в точке А.
Докажем, что точка А – искомая, т.е является точкой пересечения параболы и прямой PQ.
То что она лежит на прямой PQ следует из построения.
Для доказательства равенства AB=AF имеем пока следующее (см. рисунок):
1) Угол BFС равен углу EDC (обозначим их через α )
2) Угол FBC равен углу DEC (они равны 90-α )
3) Так как углы ABC и DCF прямые, то ABF=90-(90- α )= α .
Осталось доказать, что угол AFВ равен α.
Кто возьмется?











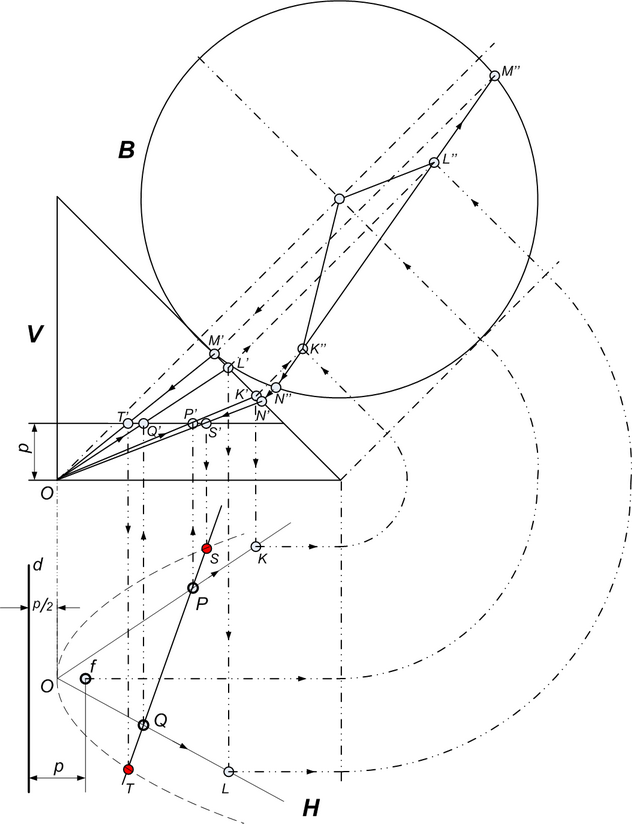
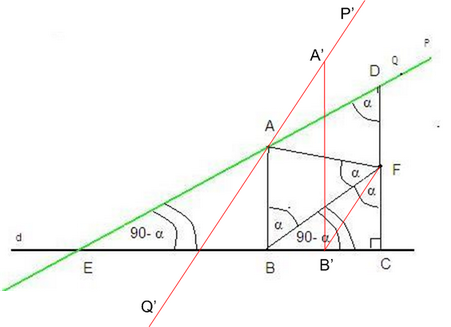
 Линейный вид
Линейный вид
