Похождения хорды

[Наташа]

Сообщение от Shuhrat Ismailov

Могу доказать, что существует аффинное преобразование, переводящее этот эллипс в окружность

Да, при афинном преобразовании отношение MQ/NQ должно сохраниться -поскольку MQ, NQ лежат на одной прямой...

[Shuhrat Ismailov]

Сообщение от Наташа

Да, при афинном преобразовании отношение MQ/NQ должно сохраниться -поскольку MQ, NQ лежат на одной прямой...

Пусть ABCD – чётырёхугольник, а диагонали AC и BD пересекаются в точке Q.
Обозначим:
AQ =a, QC=c, BQ=b, QD=d, х=(ac/bd)^(1/2) (*).
Рассмотрим четырёхугольник AB´CD´ такой, что B´D´ лежит на прямой BD, B´ Q =b’, QD’=d’, причём
b’=xb, d’=xd (**).
Тогда, так как Q делит диагонали AB´CD´ так же, как диагонали ABCD, то A´BC´D переводится аффинным преобразованием в ABCD.
Из (*) и (**) следует AQ•QC=B’Q•QD’, т.е. около AB´CD´ можно описать окружность.
Тогда при преобразовании эта окружность переходит в эллипс, описанный около ABCD. Преобразование, обратное данному, тоже является аффинным.

Таким образом, остается решить задачу:
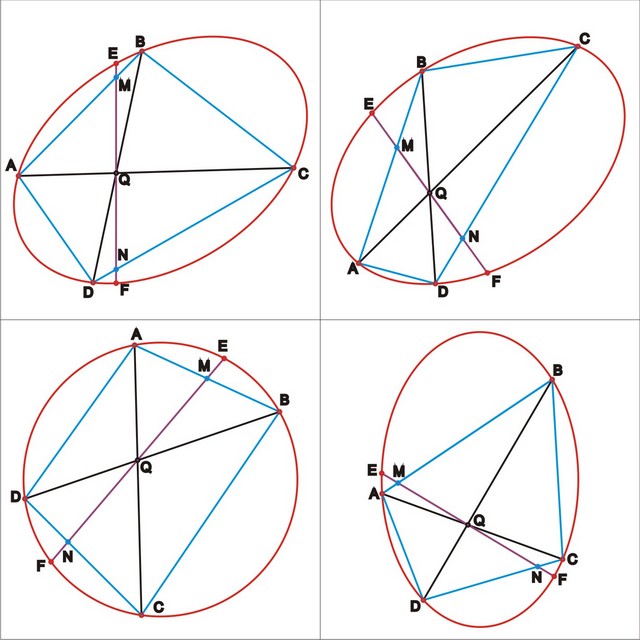
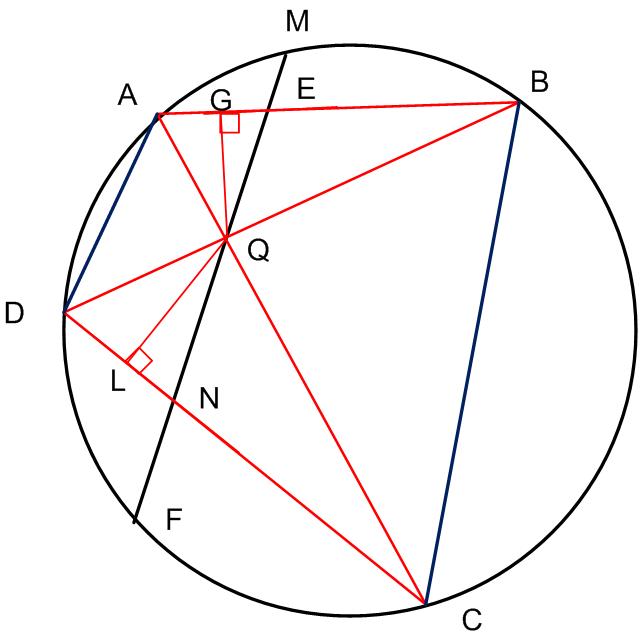
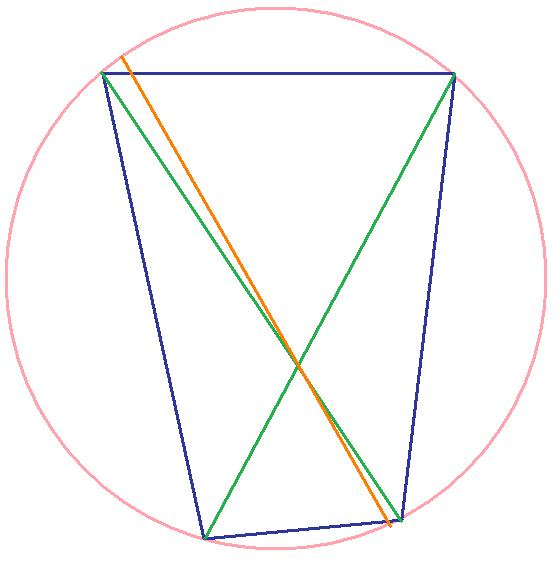
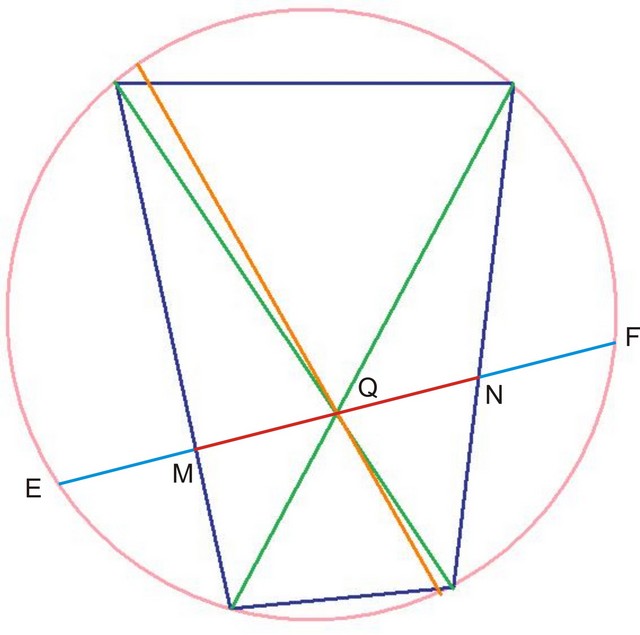
Точка Q пересечения диагоналей вписанного в окружность четырехугольника ABCD делит пополам хорду EF. EF пересекает стороны AB и CD четырехугольника в точках M и N соответственно. Можно ли доказать, что отрезки MQ и NQ равны?

[b_a_lamut]

Сообщение от Barbedo

В условии не говорится о том, что хорда EF проходии через центр эллипса.

Строится легко, значит есть закономерность. Интересно, почему это её (закономерность) никто не опровергает

[Nadir Zaitov]

Кстати, учитывая, что EF произвольная хорда, проходящая через точку Q, то не значит ли равенство NQ=MQ равенству AQ=QC и DQ=QB??? А раз это выполнено не всегда, то ясно, что утверждение не всегда верно. Кажется так.

[Barbedo]

Сообщение от Nadir Zaitov

Кстати, учитывая, что EF произвольная хорда, проходящая через точку Q, то не значит ли равенство NQ=MQ равенству AQ=QC и DQ=QB??? А раз это выполнено не всегда, то ясно, что утверждение не всегда верно. Кажется так.

Неубедительно. Для иллюстрации этого "не всегда" могли бы Вы привести пример, построить случай, когда чертеж удовлетворяет условиям, но при этом NQ<>MQ?

[Наташа]

после Афинных преобразований проделанных Shuhrat Ismailov, все будет выглядеть примерно так:
а триугольники DQC и ABQ, будут подобными и DQL, GEQ тоже подобны -равенство же их я еще посмотрю...

[Barbedo]

Сообщение от Наташа

после Афинных преобразований проделанных Shuhrat Ismailov, все будет выглядеть примерно так:
а триугольники DQC и ABQ, будут подобными и DQL, GEQ тоже подобны -равенство же их я еще посмотрю...

Ваш чертеж хорош, Наташа, но боюсь, как бы он не ввёл Вас в заблуждение. По условию точка Q - середина хорды эллипса EF, что должно сохраниться, видимо, и после афинного преобразования, и этот факт может сыграть определенную роль в решении задачи.

[Наташа]

Сообщение от Наташа

а триугольники DQC и ABQ, будут подобными и DQL, GEQ тоже подобны -равенство же их я еще посмотрю...

-NQL

[Nadir Zaitov]

Сообщение от Barbedo

Неубедительно. Для иллюстрации этого "не всегда" могли бы Вы привести пример, построить случай, когда чертеж удовлетворяет условиям, но при этом NQ<>MQ?

Я не подписал картинку. Может и не прав, но вроде б все получается как надо.

[b_a_lamut]

Сообщение от Nadir Zaitov

Я не подписал картинку. Может и не прав, но вроде б все получается как надо.

Может и ошибаюсь, но, наверное имеется в виду это: