Докажем теорему Нагеля

[b_a_lamut]

Чертёж условия. Для наглядности. Безвозмездно

[b_a_lamut]

Продолжим прямую А1В1 до пересечения с окружностью в точках Е и D. Точки Е и D соединяем с центром окружности и получаем равнобедренный треугольник DOE с основанием DE. Соединяем точки Е и D с точкой С. Получаем треугольник DCE. Доказываем, что треугольники DCO и ECO равны и, что треугольник DCE тоже равнобедренный, с тем же основанием – DE. Прямая линия, в равнобедренном треугольнике, заключённом в описанную окружность и, проходящая через вершину треугольника и центр окружности является для этого треугольника медианой, биссектрисой и высотой. Со всеми вытекающими последствиями. Или, что-то не доказано?

[Barbedo]

Сообщение от b_a_lamut

Доказываем, что треугольники DCO и ECO равны

Каким образом?

[b_a_lamut]

Сообщение от Barbedo

Каким образом?

Точно. Сложно, да и не нужно.

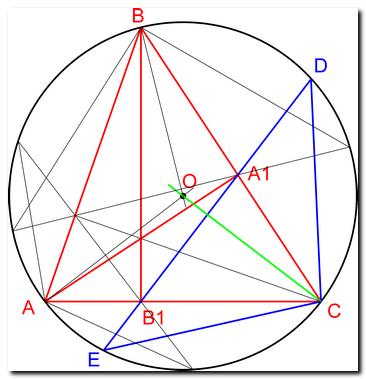
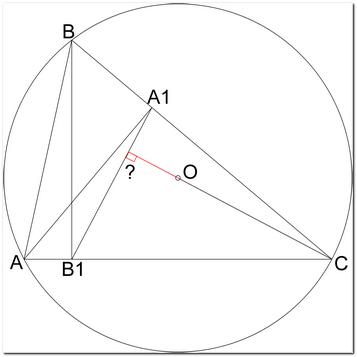
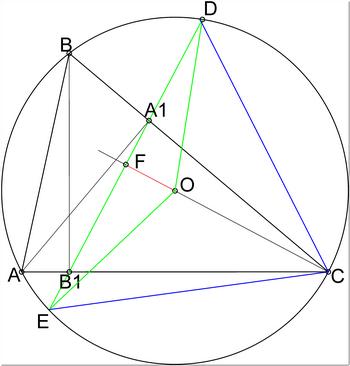
Вот, гораздо проще. Если между двумя точками пересечения высот со сторонами описанного треугольника (А1 и В1) провести прямую до пересечения с данной окружностью ( точки D и E), то эти точки будут равноудалены от вершины треугольника из которого высота не проведена (точка С). Эта теорема, наверное давно доказана. Значит треугольник DCE равнобедренный. Если через вершину равнобедренного описанного треугольника и центр окружности провести прямую, то она и предстанет перед нами во всех трёх ипостасях (Эта теорема, наверное тоже давно доказана). А так как прямая А1В1 лежит на стороне треугольника то и СО будет перпендикулярна А1В1

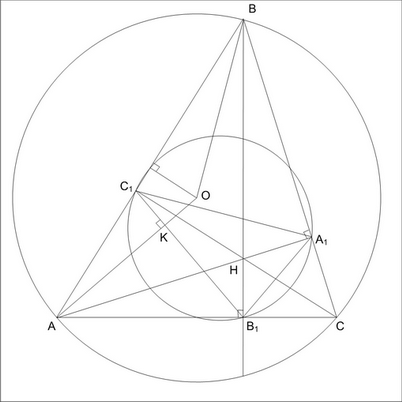
Чёрными тонкими линиями – для остальных двух случаев. Неужто опять пошёл по неправильному пути?

[Timofeus]

Сообщение от b_a_lamut

Вот, гораздо проще. Если между двумя точками пересечения высот со сторонами описанного треугольника (А1 и В1) провести прямую до пересечения с данной окружностью ( точки D и E), то эти точки будут равноудалены от вершины треугольника из которого высота не проведена (точка С). Эта теорема, наверное давно доказана.

У меня ощущение, что она доказана Нагелем .

[b_a_lamut]

Сообщение от Timofeus

У меня ощущение, что она доказана Нагелем .

Я говорил о двух других теоремах. Их авторов, к сожалению не знаю. А вообще-то, Пифагор когда ещё скроил штаны, а миллионы детишек до сих пор учатся у него кроить и заново доказывают, чтобы убедиться, что его выкройка совершенна и модна на все времена

[Timofeus]

Сообщение от b_a_lamut

Я говорил о двух других теоремах.

Я имел в виду, что утверждение

Сообщение от b_a_lamut

эти точки будут равноудалены от вершины треугольника из которого высота не проведена...

исходит из того , что СО и ЕД перпендикулярны, что и является предметом теоремы.

[b_a_lamut]

Сообщение от Timofeus

исходит из того , что СО и ЕД перпендикулярны, что и является предметом теоремы.

Интересно посмотреть решение Barbedo. У него всегда красивые решения

[Barbedo]

Сообщение от b_a_lamut

Интересно посмотреть решение Barbedo. У него всегда красивые решения

Благодарю за сарказм, коллега

Решал таким образом:

Поскольку угол ортотреугольника C1=A+B-C=180°-2С и C1H является его биссектрисой, то угол CC1B1=90°-C. Тогда угол AC1B1 = C. С другой стороны угол AOB=2C, соответственно угол С1AO=90°-C. Следовательно, угол C1KA= 180° - AC1B1 - С1AO=90°.

Но о существовании этой теоремы рассказал мне Николай Москвитин. Хорошо бы найти и поглядеть, как доказал теорему сам Нагель.

[b_a_lamut]

Сообщение от Barbedo

Благодарю за сарказм, коллега

Ой, никакого сарказма Всегда с нетерпением жду ваши задачи и красивые решения, особенно в области геометрии. Они для меня наиболее интересны, так как в них я наименее компетентен. С вашим доказательством буду разбираться (пока не могу охватить весь объём сразу).

Коллега, скажите, что в моём решении осталось не доказанным? Ваши замечания важны для меня. С уважением, b_a_lamut.