Цитата:
Сообщение от Evgeniy Sklyarevskiy

Шухрат, я ответ не знаю, привел задачу только из-за красивого условия.
|
Задача, по моему до конца не решенная.
Провел небольшое историческое исследование вопроса.
Название "Задача о числе связных графов, с точностью до гомеоморфизма , которые можно построить на плоскости, используя грани единичной длины"
На известном сайте
http://mathworld.wolfram.com/MatchProblem.html
есть коротенькая статья об этом
Цитата:
Match Problem.
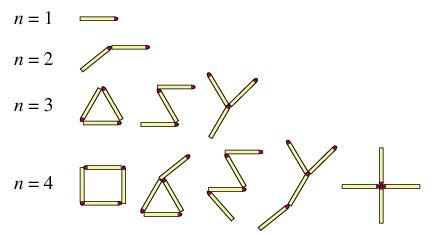
Given matches (i.e., rigid unit line segments), find the number of topologically distinct planar arrangements which can be made (Gardner 1991). In this problem, two matches laid end-to-end with no third match at their meeting point are considered equivalent to a single match, so triangles are equivalent to squares, -match tails are equivalent to 1-match tails, etc.
Solutions to the match problem are planar topological graphs on edges, and the first few values for , 1, 3, 5, 10, 19, 39, ... (Sloane's A003055).
REFERENCES:
1) Gardner, M. "The Problem of the Six Matches." In The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University Press, pp. 79-81, 1991.
Оффтоп: (Перевод: Неожиданная казнь и другие математические развлечения - внимание, можно подумать, что вешать человека - это одно из развлечений математиков! прим. моё)
Оффтоп: Эту книгу , как и другие книги Гарднера скачать можно здесь
2) Sloane, N. J. A. Sequence A003055/M2464 in "The On-Line Encyclopedia of Integer Sequences."
|
Кстати, я ошибся кажется в случае 6.





 ЕС
ЕС




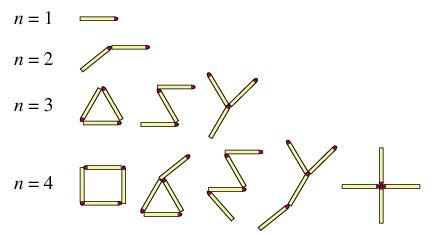
 Линейный вид
Линейный вид
