Построить точку пересечения прямой и окружности

[Timofeus]

Сообщение от Barbedo

А есть вопрос №4?

Сообщение от Barbedo

Из H опускаем перпендикуляр на AC.

Не?

[Barbedo]

Сообщение от Timofeus

Не?

Пояснение №4.

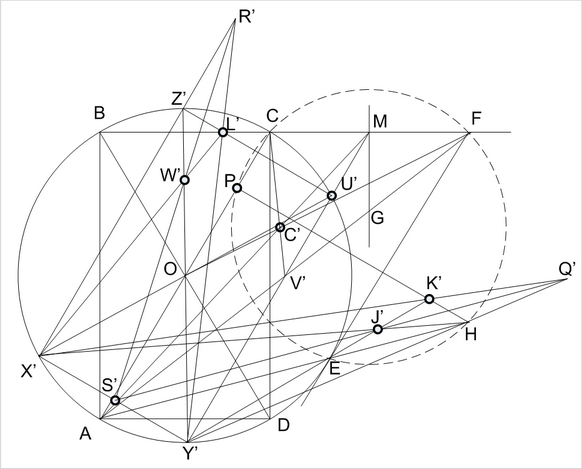
Для построения перпендикуляра к AC через точку H нам необходимо сначала построить хорду окружности, параллельную искомому перпендикуляру, а для этого нужно построить секущую окружности, отличную от диаметра, параллельную AC. Выберем отрезок AC в качестве основания трапеции с известной серединой в точке O. Пусть F будет пересечением продолжений ее сторон, а M - одной из вершин второго основания. Проведем AF, AM и OF. Точка C’ пересечения OF и AM является точкой пересечения диагоналей трапеции. Проводим CC’ до пересечения с AF в точке V’ - второй вершине основания MV’ трапеции ACMV’. Проводим секущую MV’ и отмечаем точки ее пересечения с окружностью U’ и Y’. Через O проводим диаметры U’X’ и Y’Z’. Тогда X’Y’ и U’Z’ параллельны искомому отрезку HP. Найдем точку S’ - середину X’Y’ с помощью трапеции X’Y’Z’L’, где L’ - произвольная точка на отрезке U’Z’. Проведем теперь Y’H и на его продолжении отметим произвольную точку Q’, которую используем как пересечение продолжений сторон трапеции с основанием X’Y’. Проведем X’Q’. Проведем S’Q’ и X’H и через точку их пересечения J’ проведем Y’J’. На пересечении Y’J’ и X’Q’ найдем вторую вершину K’ основания HK’ трапеции X’K’HY’. Наконец, проводим HK’ до пересечения с AC в искомой точке P.