Цитата:
Сообщение от b_a_lamut

Нельзя ли показать наглядно?
|
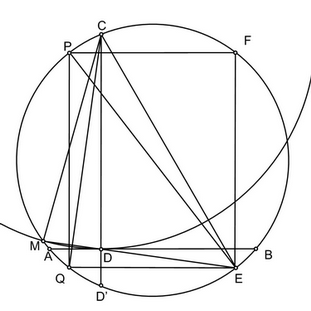
Раствором циркуля СD проведем дугу до пересечения с исходной окружностью в точке M. Проведем луч MD до пересечения с исходной окружностью в точке E.
Поскольку CM=CD, искомый отрезок EF будет виден из любой точки окружности под тем же углом, что и CM. Проведем CQ перпендикулярно MD и QP перпендикулярно AB. Тогда <QEM = <QCM = <QCD = <PQC = <PEC. Соответственно, PC=MQ и <MEC = <QEP, следовательно, PQ=CM. Если же провести EF || QP, то EF будет перпендикулярен AB и равен PQ и MC. Таким образом, любая из вершин прямоугольника PQEF удовлетворяет условию задачи для искомой точки E, но в два шага оказалось проще всего построить точку E на продолжении MD.










 Нельзя ли показать наглядно?
Нельзя ли показать наглядно?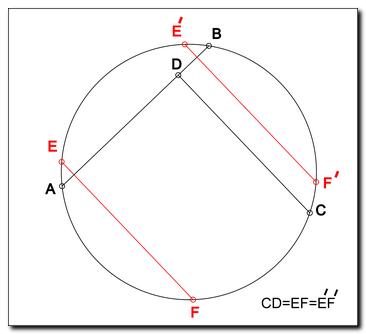

 Линейный вид
Линейный вид
