Цитата:
Сообщение от Nadir Zaitov

Цитата:
Сообщение от Barbedo

Видимо, нуобходимо уточнить условие: пляж занимает лишь определенный отрезок правого берега:
|
Интересно, если задачу перефразировать как "провести окружность через две данные точки В и С так, чтобы она касалась прямой AD", то решить должно быть будет легче. |
Верно, ваша переформулировка эквивалентна исходной.
Цитата:
Сообщение от Evgeniy Sklyarevskiy

Может так случиться, что ни одна окружность, проходящая через эти точки, не коснется второго берега...
|
По-видимому, это не так.
Точку касания всегда можно найти. Именно, если точка D на берегу, не содержащему отрезок BC, такова, что AD^2 =AB•AC, то AD — касательная к окружности.
Аналогичная задача, приближенная к условиям Узбекистана, в которой нет бухт:
Берега реки представляют из себя параллельные прямые. Найти на берегу реки точку, из которой пляж, расположенный на другом берегу, виден под наибольшим углом.









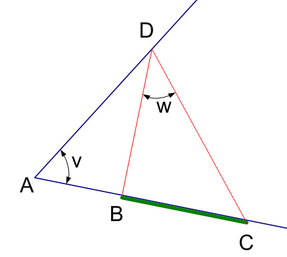






 В нашем случае мы не считаем прямую бесконечно большой окружностью
В нашем случае мы не считаем прямую бесконечно большой окружностью  Линейный вид
Линейный вид
