Пусть даны прямые g, w и точка P.
Воспользуемся теоремой Дезарга:
Если два треугольника расположены так, что прямые, соединяющие их соответсвенные вершины, проходят через одну точку, то точки пересечения соответственных сторон этих треугольников коллинеарны.
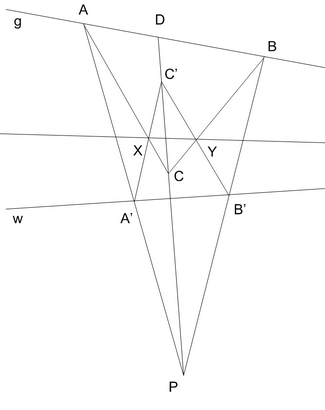
Проведем из точки P три луча через произвольно выбранные на прямой g точки A,B и D между ними. Точки A’ и B’ отметим на прямой w, а вершины C и C’ треугольников выберем произвольно на прямой PD. Треугольники ABC и A’B’C’ готовы, остается провести прямую через точки X (пересечения сторон AC и A’C’) и Y (пересечения сторон BC и B’C’), тогда прямая XY пройдет и через недоступную на чертеже точку Z пересечения данных прямых g и w (сторон AB и A’B’ треугольников).



















 Линейный вид
Линейный вид
